CÁLCULO VECTORIAL: NOVIEMBRE

CLASES DE CURVATURA

CURVATURA DE FLEXIÓN(k)

La curvatura de flexión o simplemente curvatura se define como:

El radio de curvatura de flexión se define como:

-Se llama radio de curvatura de flexión al inverso de la curvatura de flexión.

-La curvatura de flexión es la razón de cambio de dirección del vector T de un punto a otro punto.

CURVATURA DE TORSIÓN(T)

La torsión nos indica el alejamiento o acercamiento de la curva a un plano osculador.

-Las curvaturas de flexión y de torsión se calculan también:

FUNCIONES ESCALARES DE VARIAS VARIABLES

f : R^n → R

(X1,X2,...Xn) → u=f(X1,X2,...Xn)

-En R^2 :

f : R^2→ R

(x,y) → Z=f(x,y)

x,y: v. independientes

z: v. dependientes

- En R^3 :

f : R^3→ R

(x,y,z) → W=f(x,y,z)

x,y,z: v. independientes

w: v. dependientes

FUNCIONES DE DOS VARIABLES:

En R^2:

f : R^2→ R

(x,y) → Z=f(x,y)

- El dominio de la función de f(x,y) se define : Df={(x,y) E R^2/Z=f(x,y) }

- El dominio es todo el plano XOY o una región de este plano.

- La representación gráfica de Z=f(x,y) es una superficie en el espacio.

Descripción:

El análisis de domino o campo de existencia de una función f(x,y). Se realiza de la siguiente forma :

1. Analítico.

2. Gráfico en R^2 y R^3.

3. Descriptiva.

GRÁFICAS

- Si f es una función de dos variables con dominio D, entonces la gráfica de f es el conjunto de todos los planos (x,y,z) en R^3 tal que Z=f(x,y), siendo (x,y) elemento del dominio.

CURVAS DE NIVEL:

- La curvas de nivel de una función f(x,y) son las curvas cuyas ecuaciones son f(x,y)=K, donde K es una constante (en el rango de f).

- Las curvas de nivel sirve para realizar la topo logia de una región.

-Si la función f(x,y) representa:

i) La función temperatura, las curvas de nivel de nivel se denominan isotermas.

ii) La función potencia → equipotenciales.

iii)La función presión → Isobaras.

- Si las curvas de nivel se representa en 3D, entonces se denomina curvas de entorno

LIMITES Y CONTINUIDAD

f : R^2→ R

(x,y) → Z=f(x,y)

Dada

f∈Φ={f:A⊆R⟶R}una función real de variable real y dado

a∈R, decimos que el limite de la función f en el punto a∈R es el número

L∈R, que representamos por:

limf(x)x→a=L∈R y que definimos por:

limf(x)x→a=L∈R⇔{∀ε>0,∃δ>0/∀x∈A,d(x,a)<δ⇒d(f(x),L)<ε}

Para las funciones de 2 variables, el dominio es una parte o todo el plano XOY, por tanto existe infinitas caminos o trayectoria de acercamiento.

- Si por 2 caminos diferentes el valor del limite toma diferente valor, podemos concluir que el limite no existe.

- Si por 2 o mas caminos diferentes el limite toma el mismo valor "L", se supones que el limite existe y debe proceder a demostrarlo.

- Para demostrarlo que f(x,y) es continua en (a,b), entonces debe cumplir :

Existen dos tipos de discontinuidad:

1) Evitable
- f(x) no es continua si existe un x=a perteneciente al Dom(f) tal que

- En este caso se debe redefinir la función para obligarla a cumplir la condición que se cumple.

2) Inevitable

Si no esiste:

DERIVADA PARCIALES

En matemática, una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.

EJEMPLO:

DERIVADAS PARCIALES DE SEGUNDO ORDEN

Se llaman derivadas parciales de segundo orden de la función z=f(x,y) a las derivadas parciales de las derivadas parciales de primer orden.

TEOREMA DE CLAIRAUT

En matemáticas y más concreta mente en cálculo diferencial el teorema de Clairaut, también conocido como teorema de Schwarz o teorema de la igualdad de las derivadas cruzadas es una condición suficiente de la igualdad de las derivadas parciales cruzadas de una función de varias variables. El teorema establece que si las derivadas parciales cruzadas existen y son continuas, entonces son iguales.

REGLA DE LA CADENA

Caso de una variable independiente:

Sea z=F(x,y) una función suave, es decir, con derivadas parciales continuas y supongamos que tanto x como y son funciones de un parámetro t y ambas tienen derivadas respecto de t. Entonces z=F(x(t),y(t)) es una función compuesta. Un cambio en t afectará a las variables x e y, por lo tanto se producirá un cambio en z. Es razonable preguntarse por la razón de cambio de z respecto a t. Esta derivada puede obtenerse:

dz dt = ∂ z ∂ x . dx dt + ∂ z ∂ y . dy dt

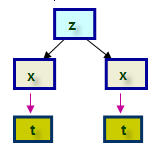
Caso de dos variables independientes

Sea z=F(x,y) una función suave, es decir, con derivadas parciales continuas y supongamos que tanto x como y son funciones de dos parámetros, s y t, existiendo también sus derivadas parciales respecto a estas variables. Entonces z=F(x(t,s),y(t,s)) es derivable parcialmente y se cumple:

∂z ∂s = ∂z ∂x ⋅ ∂x ∂s + ∂z ∂y ⋅ ∂y ∂s ∂z ∂t = ∂z ∂x ⋅ ∂x ∂t + ∂z ∂y ⋅ ∂y ∂t

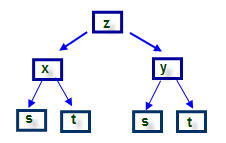
DERIVACIÓN PARCIAL IMPLÍCITA:

En la matemática la derivada parcial implícita corresponde a una función que tiene diversas variables, en este caso es una derivada con respecto a una de las variables manteniendo todas las otras como constantes. Las derivadas parciales implícitas con usadas en los cálculos de vectoriales y geometría diferencial. La derivada parcial de una cualquier función f respecto a la variables x puede ser representada como:

DERIVADAS DIRECIONALES Y EL VECTOR GRADIENTE

GRADIENTE

Se llama gradiente en un punto de una función real de varias variables reales al conjunto ordenado de las derivadas parciales de esa función en un punto.

Por tanto, el gradiente de una función f (x,y,z) en el punto ( x0, y0,z0) es