MÁXIMOS Y MÍNIMOS
Se definen puntos críticos como los puntos en los que el gradiente de la función se anula
Definición . Sea A ⊆ R ^ n un conjunto abierto y
f : A → R una función con derivadas segundas continuas en A.
Se puede demostrar que los máximos y mínimos de una función son puntos críticos si se alcanzan en puntos interiores (también pueden ser máximos y mínimos puntos en la frontera, pero entonces no son necesariamente críticos)
CRITERIO DE LA SEGUNDA DERIVADA
Supongamos que las segundas derivadas parciales de F(x,y) existen y son continuas en un disco de centro (a,b) y supongamos que Fx(a,b)=0 y Fy(a,b)=0 es decir (a,b) es un punto critico de F(x,y) sea
MÍNIMOS Y MÁXIMOS OBSOLETOS
Si f es continua en un conjunto D cerrado y acotado en R^2 y acotado en R^2 entonces f alcanza un valor máximo absoluto F(x1,y1) y un valor mínimo absoluto F(x2,y2)
MÍNIMOS Y MÁXIMOS CONDICIONALES
Para determinar los valores extremos de F(x,y) sujeta a la restricción G(x,y)=k (ecuaciones de enlace) se procede a plantear
INTEGRAL MÚLTIPLE
En R^2:
En R^3
INTEGRALES DOBLES SOBRE REGIONES MAS GENERALES
Región verticalmente simple
región horizontalmente simple
TRANSFORMACIONES A INTEGRALES MÚLTIPLES
El cambio de una variable por otra es en un sentido geométrico, una transformación desde un espacio hasta otro, y es esta transformación la que exige estos ajustes. Si se utiliza una transformación que siga la relación:

Entonces se puede utilizar el jacobiano de la transformación para simplificar la integral
TRANSFORMACIÓN A COORDENADAS POLARES
CARTESIANAS - CILÍNDRICAS
El uso de coordenadas cilíndricas para transformar una integral triple, es conveniente especialmente cuando el dominio de integración presenta simetría alrededor del eje z. La función se transforma mediante la siguiente relación.

El determinante jacobiano de la transformación es el siguiente:
COORDENADAS ESFÉRICAS
Cuando existe simetría esférica en un dominio en R3, es posible utilizar una transformación hacia coordenadas esféricas para simplificar una integral triple. La función es transformada por la relación:
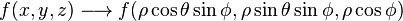
El determinante jacobiano de la transformación es el siguiente:
Tomando el valor absoluto del determinante se obtiene el factor que se debe añadir a la integral.
Por lo tanto los diferenciales dx dy dz se transforman en ρ2 sin(φ) dρ dθ dφ.
INTEGRALES TRIPLES
Referencias:
- http://www.monografias.com/trabajos78/integrales-triples/integrales-triples.shtml
- Calculo de varias variable Stewart
- http://imerl.fing.edu.uy/calculo2/archivos/NotasTeorico/IntegralesDobles3.pdf
- https://www.uam.es/personal_pdi/ciencias/fchamizo/asignaturas/quim1314/resumen02.pdf
- http://bjglez.webs.ull.es/tema4met.pdf
- http://fernandorevilla.es/blog/2014/04/18/maximos-y-minimos-condicionados-multiplicadores-de-lagrange/


















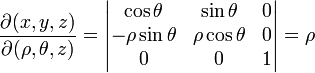

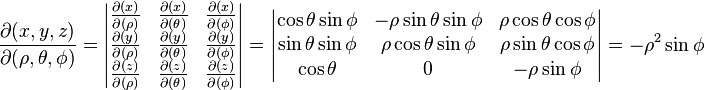


No hay comentarios:
Publicar un comentario